Create and edit run/debug configurations
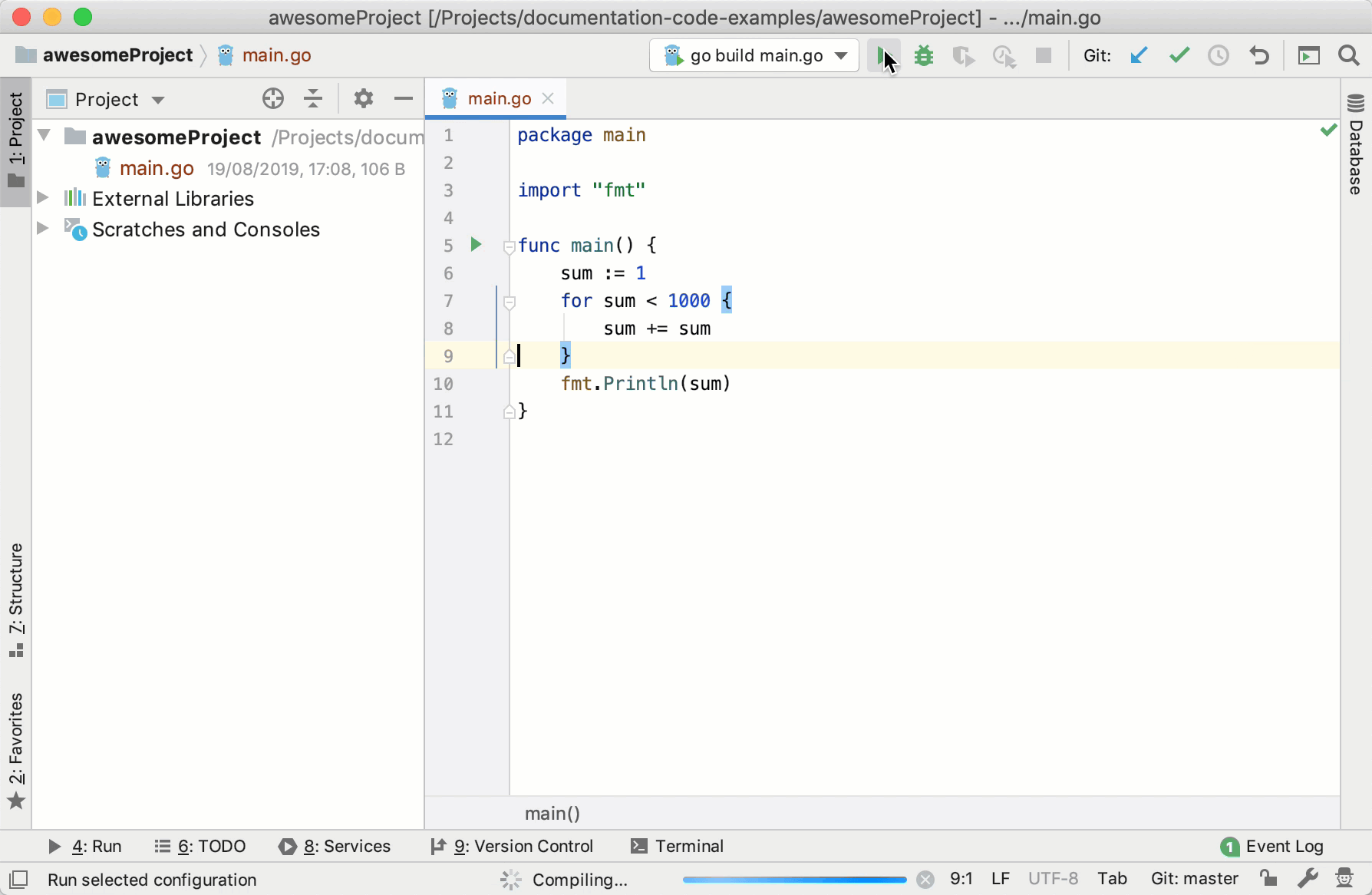
With the Navigation bar visible ( ), the available run/debug configurations are displayed in the run/debug configuration selector in the Run area:
GoLand provides the Run/Debug Configuration dialog as a tool for handling run/debug configurations: creating configuration profiles or changing the default ones.
Use the toolbar of the Run/Debug Configuration dialog to add, remove, or save configurations.
Create a run/debug configuration
Open the Run/Debug Configuration dialog in one of the following ways:
Select from the main menu.
With the Navigation bar visible ( ), choose from the run/debug configuration selector.
Press Alt+Shift+F10, then press 0 or select the configuration from the popup and press F4.
In the Run/Debug Configuration dialog, click the Add New Configuration icon (
) on the toolbar or press Alt+Insert. The list shows the default run/debug configurations. Select the desired configuration type (for example, Go build ).
The fields that appear in the right-hand pane display the default settings for the selected configuration type.
Run kind: a building scope for your application. File and Package scopes work similarly in tests and compilation/running configurations (in terms of the scope they cover).
Directory: build an application in the specified directory as a package, without processing any subdirectories.
For test configurations, GoLand runs all the tests in the specified directory and all its subdirectories.
File: build an application from files specified in the Files field. To pass multiple file paths, use the vertical bar (
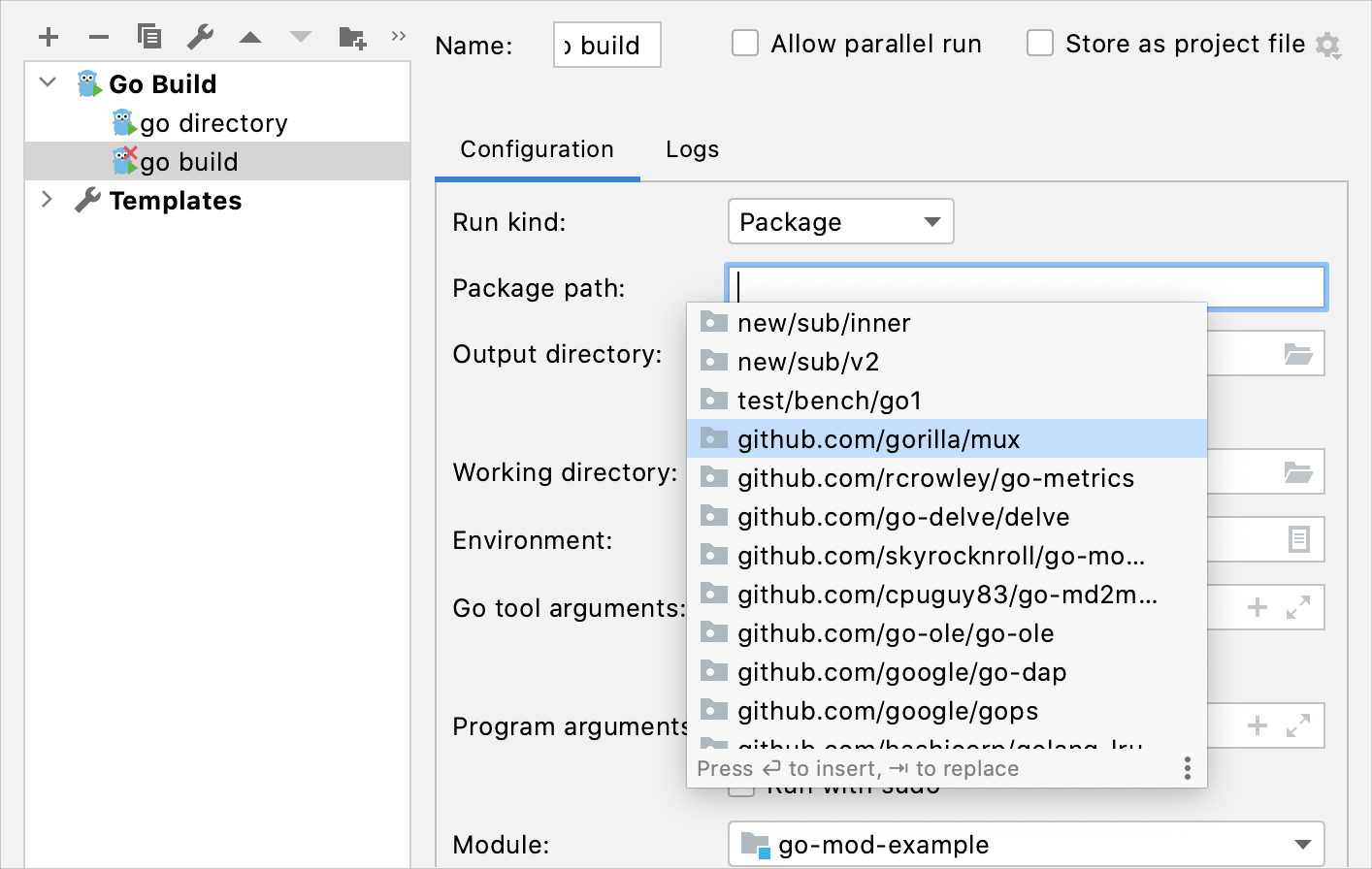
|) as a delimiter. This configuration is automatically selected when you run your program from scratch files.Package: build a single package with all its dependencies. Specify a full import path to the package that you want to build in the Package path field (for example,
github.com/gorilla/mux). This configuration is automatically selected when you run themainfunction or a separate test by using the Run icon () in the gutter.
Package path: a full import path of the package that you want to compile (for example,
github.com/gorilla/mux). This field is available only when you select the Package run kind.You can press Ctrl+Space to see a list of available packages.
Output directory: a directory for the executable file.
Run after build: execute the application after the build.
Working directory: a directory that is used for the built application. If you have any code that creates relative files or directories, they will be relative to this directory.
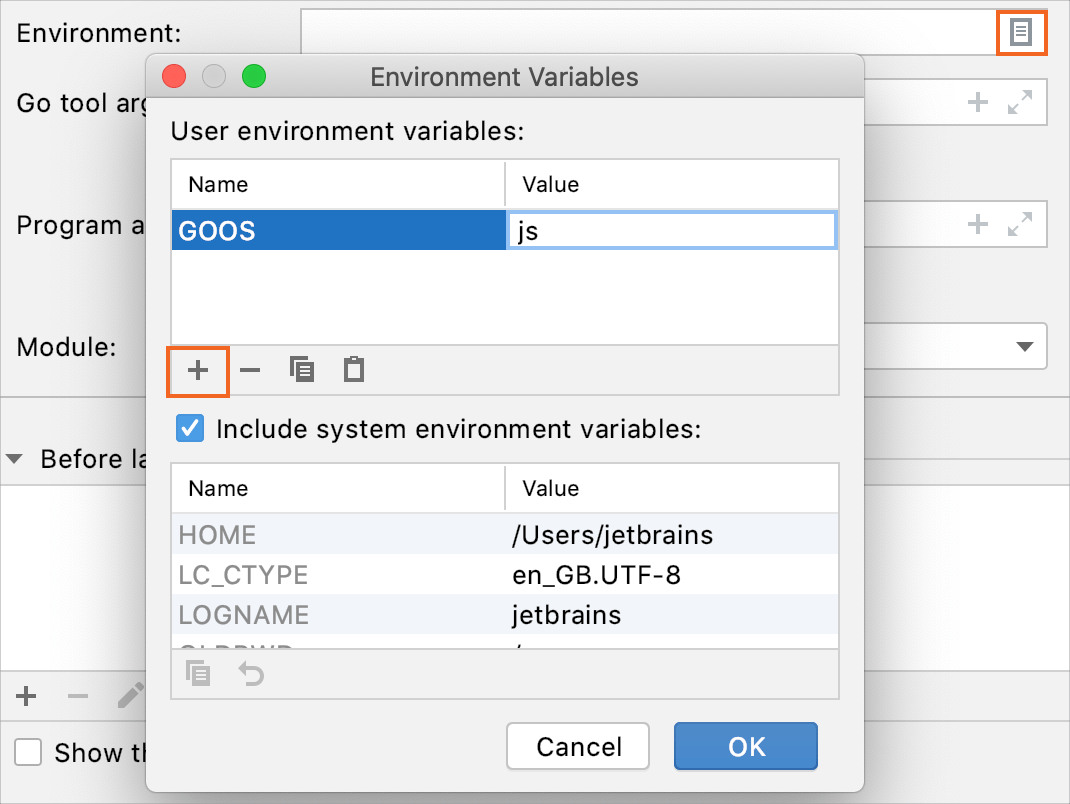
Environment: environment variables for your application.
To edit environment variables, click the Browse button at the end of the field. In the Environment Variables dialog, click the Add button and add the environment variables that you need.
Go tool arguments: arguments for the go tool (for example,
-o). Also, you can use macros in this field.Use all custom build tags: all tags that are applied during the build. Tags are listed in settings Ctrl+Alt+S under .
Program arguments: arguments for the built application. Also, you can use macros in this field.
Run with sudo: grant sudo privileges for the application.
Module: name of the current module.
Before launch: add tasks that you want to launch before the launch of the selected run/debug configuration. To add a task click the Add button Alt+Insert and select the tool that you want to add.
Store as project file: Enable this option to save your configuration as a project file and share it with team members through VCS.
Apply the changes and close the dialog.
Edit an existing run/debug configuration
- Do one of the following:
From the main menu, choose .
With the Navigation Bar visible ( ), choose from the run/debug configurations selector.
Press Alt+Shift+F10, then press 0 to display the Edit Configuration dialog, or select the configuration from the popup and press F4.
In the corresponding run/debug configuration dialog, change parameters as required.
If a project has been created in an earlier version of GoLand, its run/debug configurations can be lost, when such a project is added to another project, already opened in the same window.
To avoid the loss of run/debug configurations, it is recommended that you open such a project once in the latest version, and only after being added to another project.
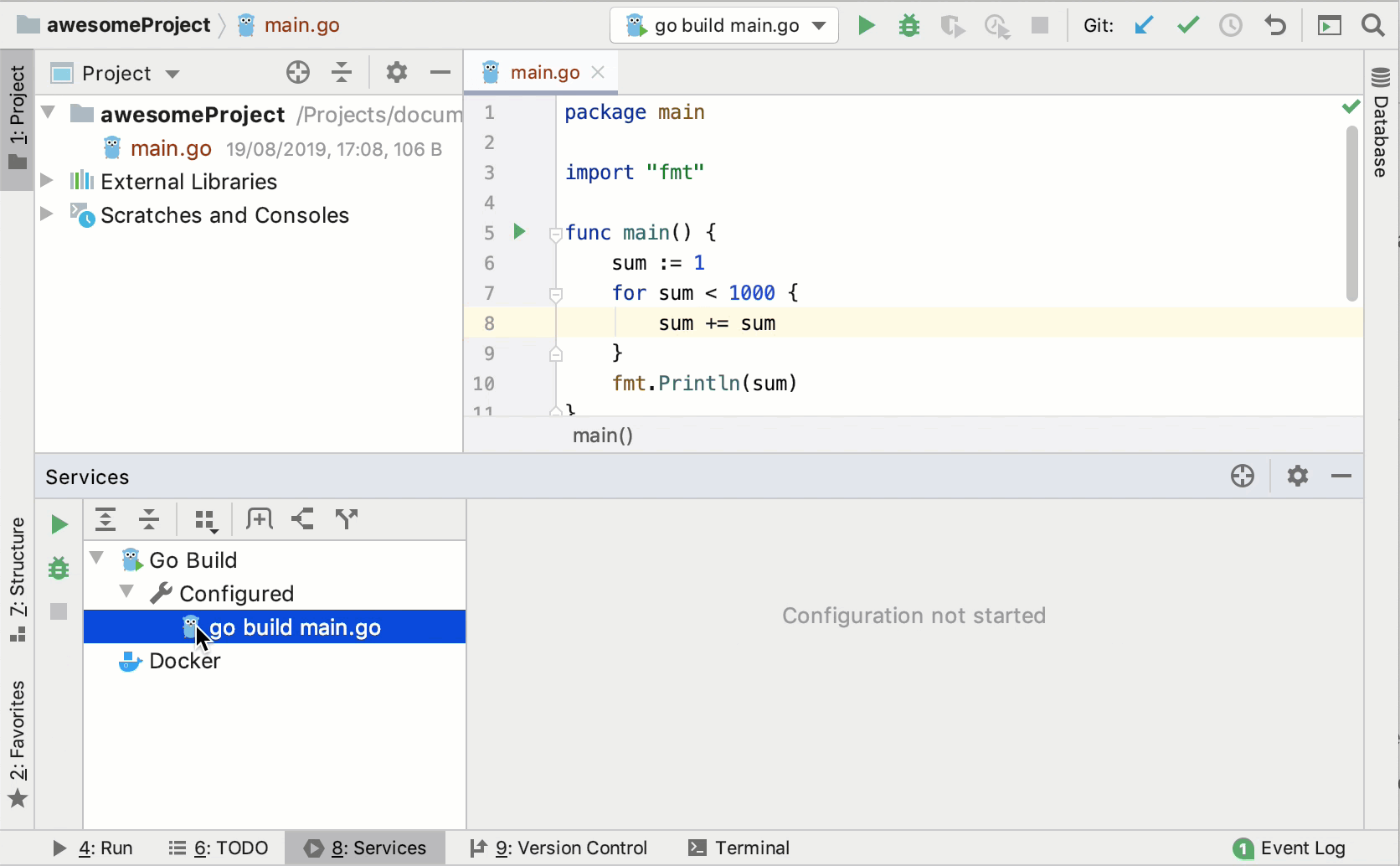
Enable the Services tool window
You can manage multiple run/debug configurations in the Services tool window. For example, you can start, pause, and stop several applications, track their status, and examine application-specific details.
From the main menu, select or use the selector on the toolbar.
In the Run/Debug Configurations dialog, select Templates from the list on the left.
In the right-hand pane, expand the Configurations available in Services section.
Click
in the Configurations available in Services section and select the necessary run configuration type.
You can add or remove multiple configuration types one by one.
Note that the tool window will only display the configuration types for which you have created one or more configurations.
Thus, if you add a configuration type for which no configurations exist in the project, this type will not be displayed in the tool window until you create a configuration of this type.
Apply the changes and close the dialog. The Services tool window with the selected configurations will open.
Share configurations
GoLand allows you to share your configurations with team members through VCS. To do this, perform the following steps:
Click .
In the Run/Debug Configuration dialog, select the required configuration and enable the Store as project file option. GoLand suggests you to create a file containing configuration settings in the .idea/runConfigurations directory.
(Optional) If the .idea directory is added to VCS ignored files, the .idea/runConfigurations subfolder will be ignored, too. If you use Git for your project, you can share .idea/runConfigurations only and leave .idea ignored by modifying .gitignore as follows:
/.idea/* !/.idea/runConfigurations
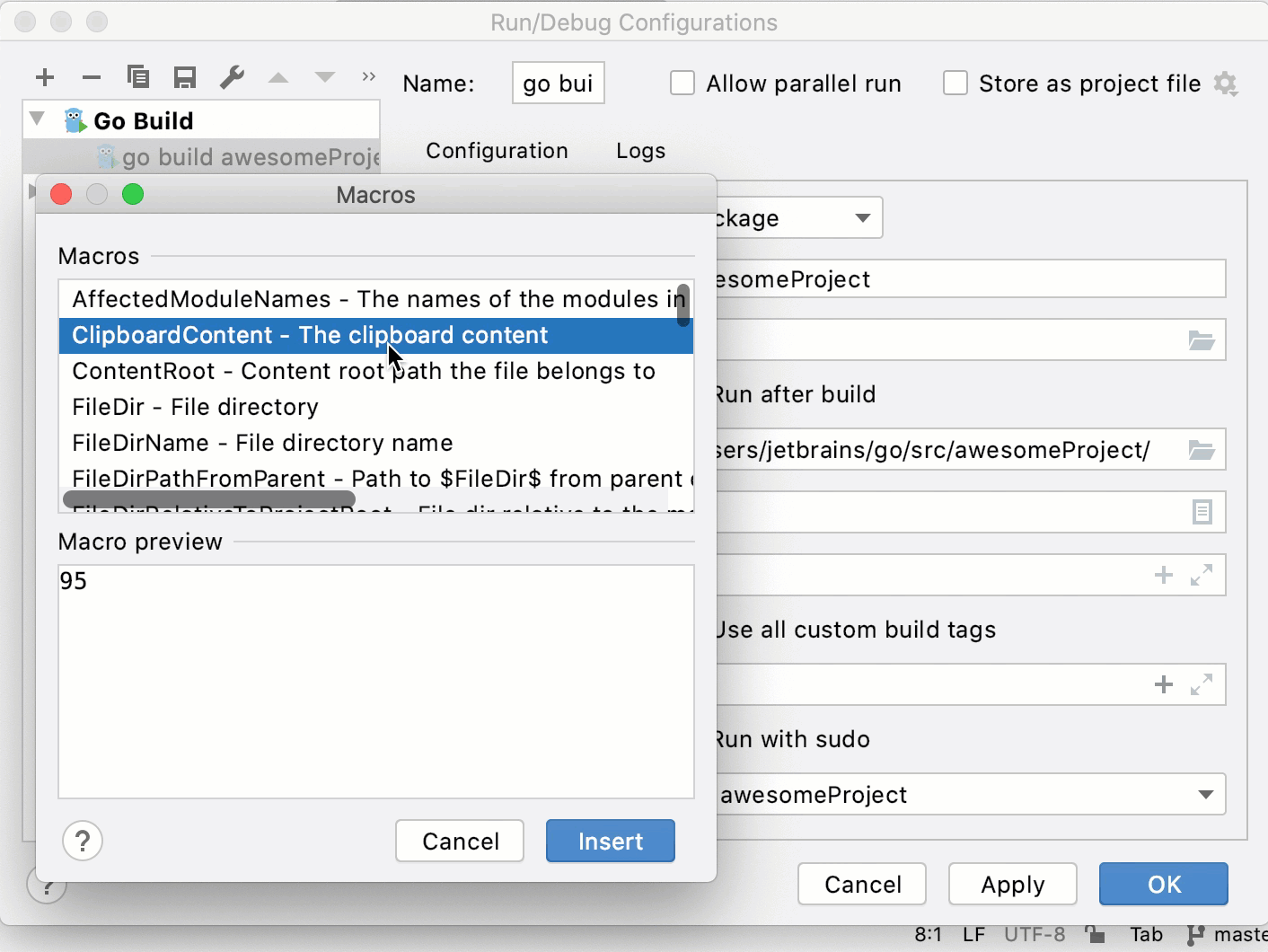
Using macros
Macros are used to make a sequence of computing instructions available to the programmer as a single program statement. In GoLand, you can use macros in Go tool arguments and Program arguments fields.
Navigate to .
Select or create a run/debug configuration in which you plan to use macros.
In Go tool arguments and Program arguments fields, click the Insert Macros icon (
).
In the Macros window, select a macro from the Macros list (for example, ClipboardContent - The clipboard content ). In the Macro preview pane, you can see the output of the macro if the output is available.
Click Insert.
See the following animation, that shows the usage of the ClipboardContent macro. You can copy the code snippet from GitHub. Before running the run/debug configuration, copy one positive number to the clipboard.