Encoding
To display and edit files correctly, GoLand needs to know which encoding to use. Source code files are usually encoded in UTF-8. This is the recommended encoding unless you have other requirements.
To determine the encoding of a file, GoLand uses the following steps:
If the byte order mark (BOM) is present, GoLand will use the corresponding Unicode encoding regardless of all other settings. For more information, refer to Byte order mark.
If the file declares the encoding explicitly, GoLand will use the specified encoding. For example, this can apply to XML, HTML, and JSP files. The explicit declaration also overrides all other settings, but you can change it in the editor.
If there is no BOM and no explicit encoding declaration in the file, GoLand will use the encoding configured for the file or directory in the file encoding settings. If encoding is not configured for the file or directory, GoLand will use the encoding of the parent directory. If the parent directory encoding is also not configured, GoLand will fall back to the Project Encoding, and if there is no project, to Global Encoding.
Change the encoding used to view a file
If GoLand displays characters in a file incorrectly, it probably couldn't detect the file encoding. In this case, you need to specify the correct encoding to be used for viewing and editing this file.
Open the file in the editor.
Click the File Encoding widget on the status bar.
Alternatively, select from the main menu.
Select the correct encoding.
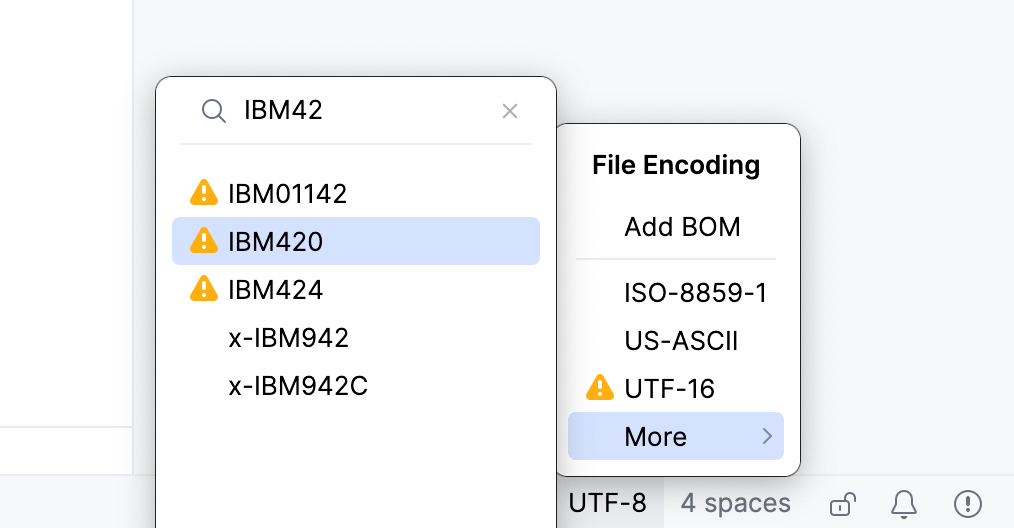
Encodings marked with
or
might change the file contents. In this case, GoLand opens a dialog where you can choose what to do with the file:
Reload: load the file in the editor from disk and apply encoding changes to the editor only. You will see the content changes related to the chosen encoding, but the actual file will not change.
Convert: overwrite the file with the chosen encoding.
This will add an association for the file to the file encoding settings. GoLand will use the specified encoding to view and edit this file.
Configure file encoding settings
Press Ctrl+Alt+S to open settings and then select .
GoLand uses these settings to view and edit files for which it was unable to detect the encoding and uses the specified encodings for new files. For more information, refer to File Encodings.
Select console output encoding
By default, GoLand uses the system encoding to view console output.
In the Settings dialog (Ctrl+Alt+S) , select .
Select the default encoding from the Default Encoding list.
Click OK to apply the changes.
For more information about console output settings, refer to Console.