Tutorial: Debug your first Kotlin application

You have created and run your Kotlin application. Let's imagine you have discovered that it functions not the way you expected. For example, it returns a wrong value or crashes with an exception. Seems like you have errors in your code, and it’s time to debug it.

What Is Debugging?

Broadly, debugging is the process of detecting and correcting errors in a program.

There are different kinds of errors, which you are going to deal with. Some of them are easy to catch, like syntax errors, because they are taken care of by the compiler. Another easy case is when the error can be quickly identified by looking at the stack trace, which helps you figure out the cause.

However, there are errors that can be very tricky and take really long to find and fix. For example, a subtle logic error, which happened early in the program may not manifest itself until very late, making it a real challenge to sort things out.

This is where the debugger is useful. It is a tool that lets you find bugs in an efficient manner by providing an insight into the internal operations of a program. This is possible by pausing the execution at a specified point, analyzing the program state, and, if necessary, advancing the execution step-by-step. While debugging, you are in full control of the things. In this manual we are covering a basic debugging scenario to get you started.

Examine the code

Let's try a simple debugging case. Imagine we have the following application:

                fun main(args: Array<String>) {
                    println("Average finder v0.1")
                    val avg = findAverage(args)
                    println("The average is $avg")
                }

                fun findAverage(input: Array<String>): Double {
                    var result = 0.0
                    for (s in input) {
                        result += s.toDouble()
                    }
                    return result
                }
            

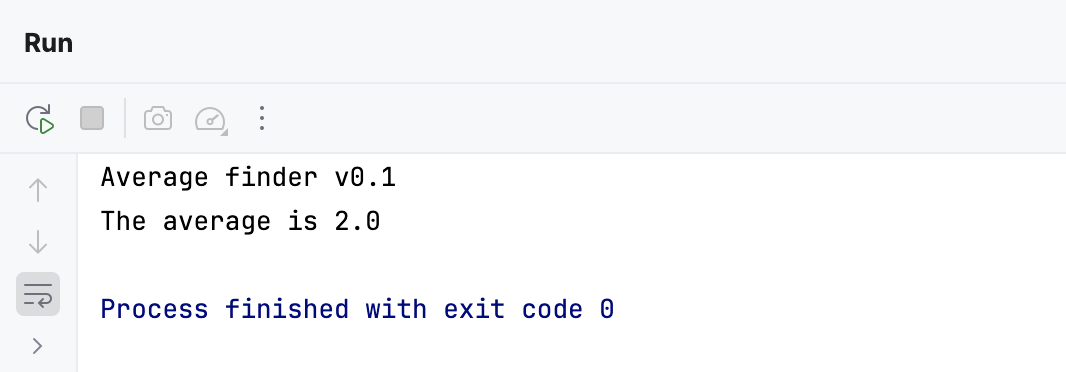
The program is supposed to calculate the average of all values passed as command-line arguments.

It compiles and runs without issues; however, the result is not what one would expect. For instance, when we pass 1 2 3 as the input, the result is 6.0.

First of all, you need to think about where the error might be coming from. We can assume the problem is not in the print statements. Most likely, unexpected results are coming from our findAverage function. In order to find the cause, let's examine its behavior in the runtime.

Set breakpoints

To investigate the bug, we need to pause the program when it reaches the piece of code that is producing a wrong result. This is done by setting breakpoints. Breakpoints indicate the lines of code where the program will be suspended for you to examine its state.

Click the gutter at the line where the findAverage function is called.

Run the program in debug mode

Now let's start the program in debug mode.

Since we are going to pass arguments for running and debugging the program, make sure the run/debug configuration has these arguments in place.

Click the Run icon in the gutter, then select Modify Run Configuration.
Enter 1 2 3 in the Program arguments field.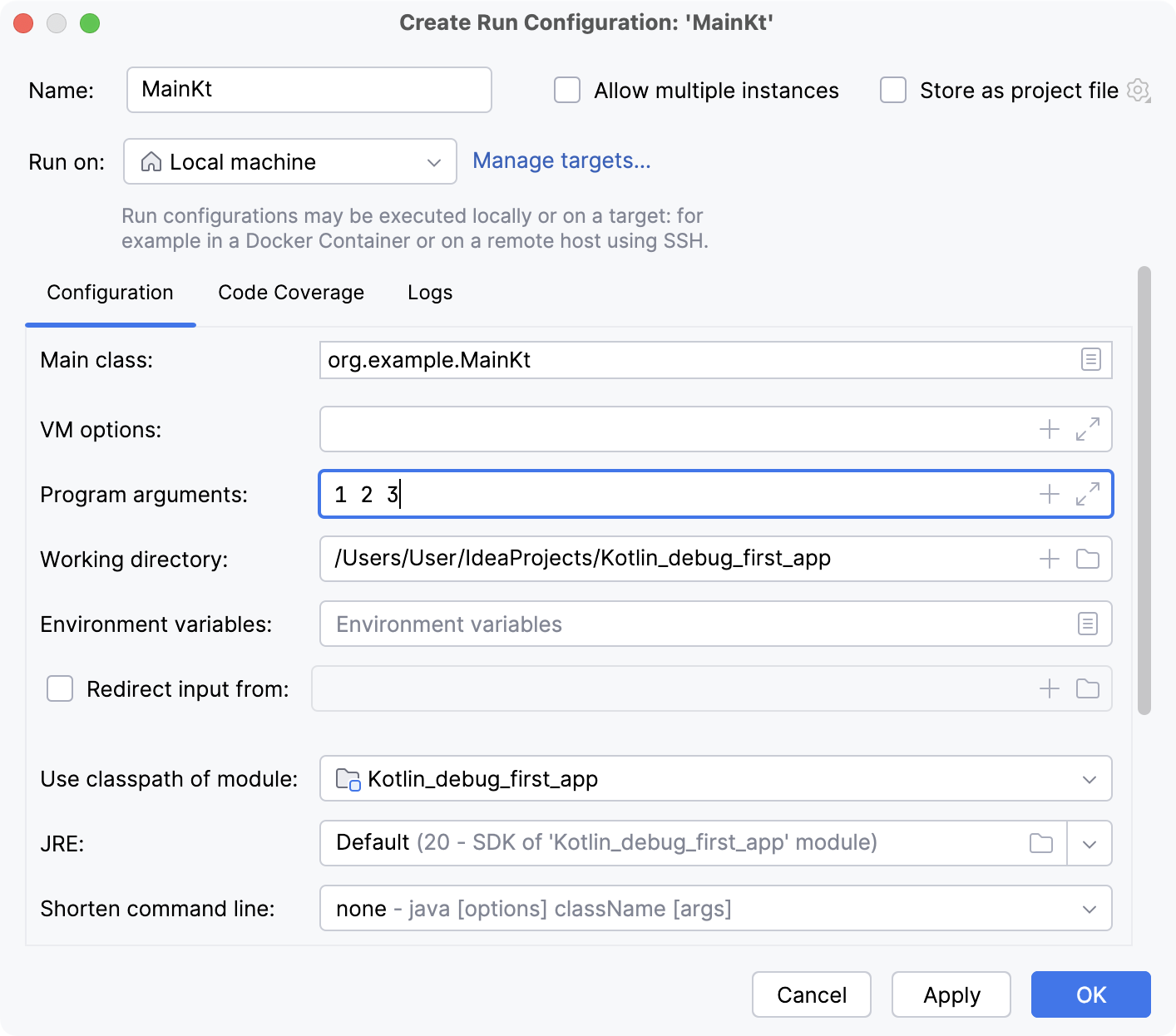
Click the Run button near the main function. From the menu, select Debug.

Analyze the program state

After the debugger session has started, the program runs normally until a breakpoint is hit. When this happens, IntelliJ IDEA pauses the program, highlights the line, at which the program is suspended, and shows the Debug tool window.

Debug tool window appears. The line with the breakpoint is highlighted

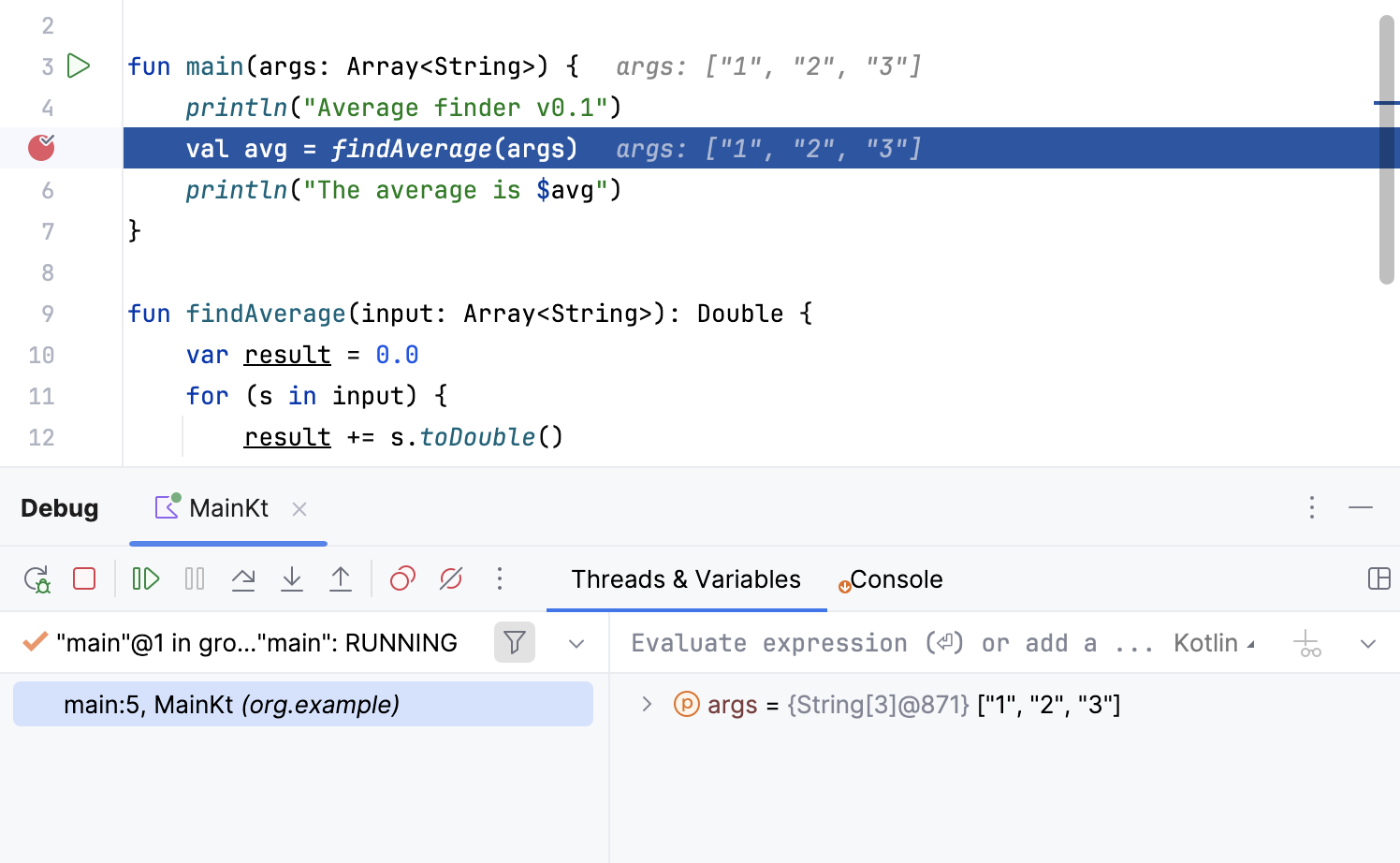
The highlighted line has not been executed yet. The program now waits for further instructions from you. The suspended state lets you examine variables, which hold the state of the program.

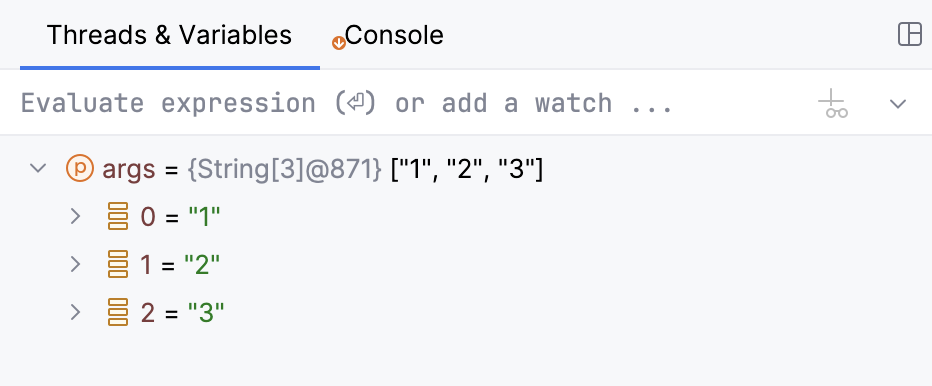
As the findAverage function has not been called yet, all its local variables like result are not yet in scope, however, we can examine the contents of the args array (args is in scope of the main function) . The contents of variables are displayed inline where args is used:

Inline debugging shows variable values right at the line where the respective variables are used

You can also get information about all variables that are currently in scope on the Threads & Variables tab on the Debug tool window.

Variable values are shown in the Variables panel

Step through the program

Now that we are comfortable with the Debug tool window, it's time to step into the findAverage function and find out what is happening inside it.

To step into a function, click the Step Into button on the Debug tool window's toolbar or press F7.
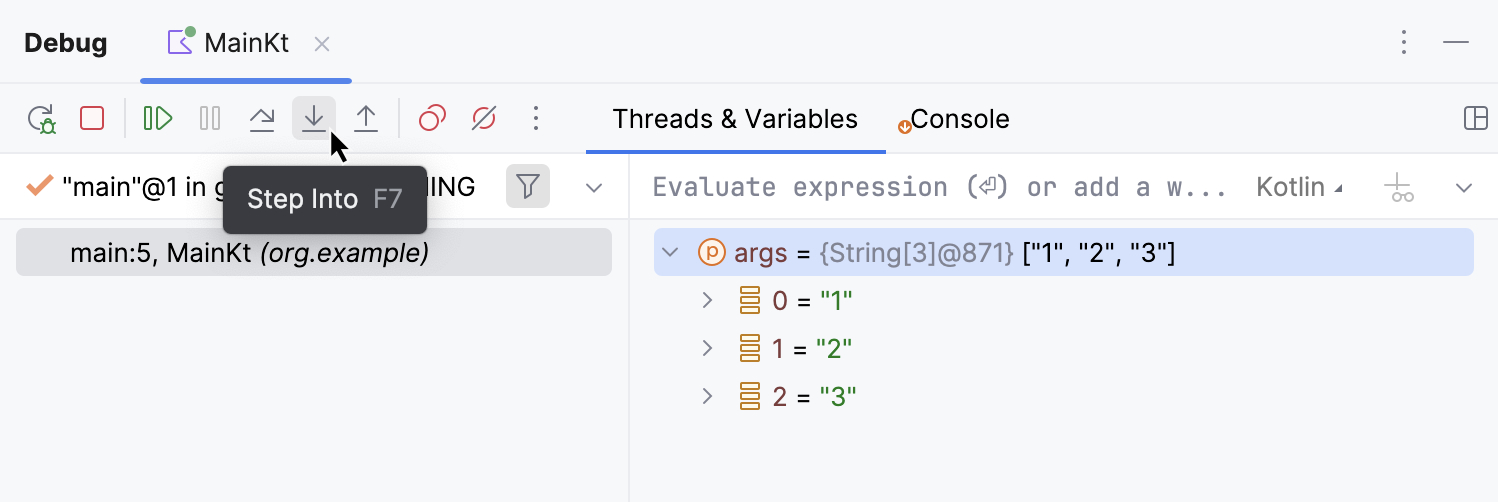
The highlighting in the editor moves to another line because we advanced the execution point one step further.
Let's keep stepping and see how the local variable result is declared and how it is changed with each iteration of the loop.
Right now the variable s contains the value "3". It is going to be converted to Int and be added to result, which currently has the value of 3.0. No errors so far. The sum is calculated correctly.
Two more steps take us to the return statement, and we see where the omission was. We are returning result, which has the value of 6.0, without dividing it by the number of inputs. This was the cause of incorrect program output.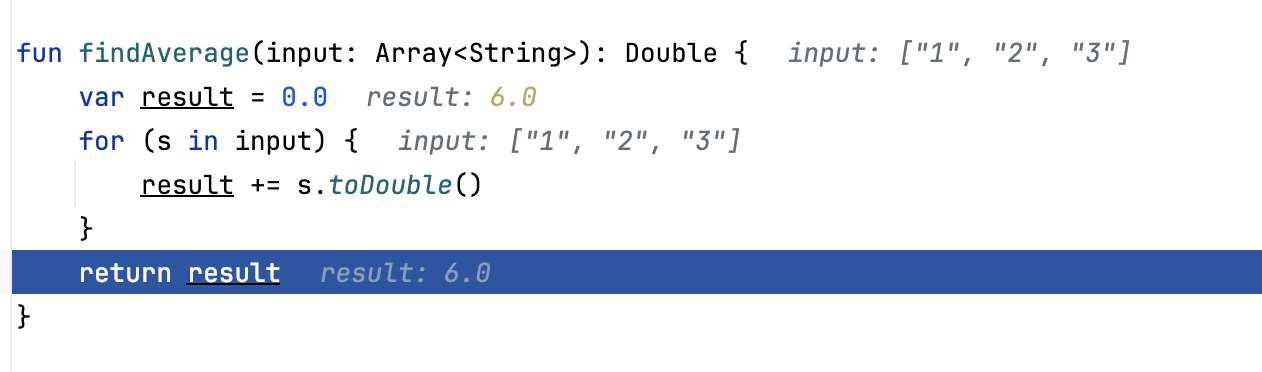
When you have finished with stepping and want to continue the program execution normally, press F9 or select Run | Debugging Actions | Resume from the main menu.
Let's correct the error:
return result / input.size

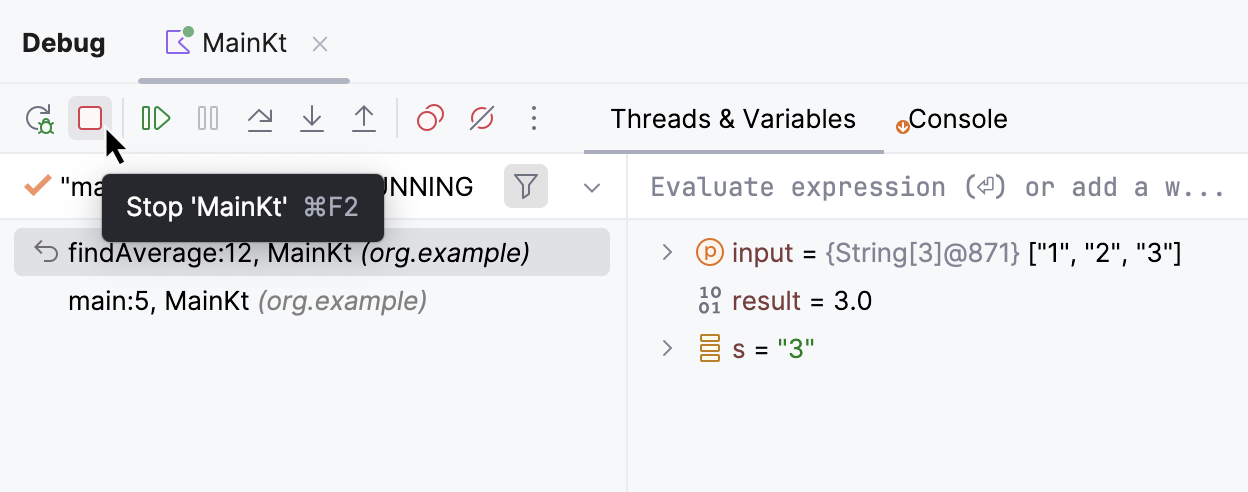
Stop the debugger session and rerun the program

To check that the program works fine, let's stop the debugger session and rerun the program.

On the Debug tool window's toolbar, click the Stop button or press Ctrl+F2.
Click the Run button near the main function. From the menu, select Run.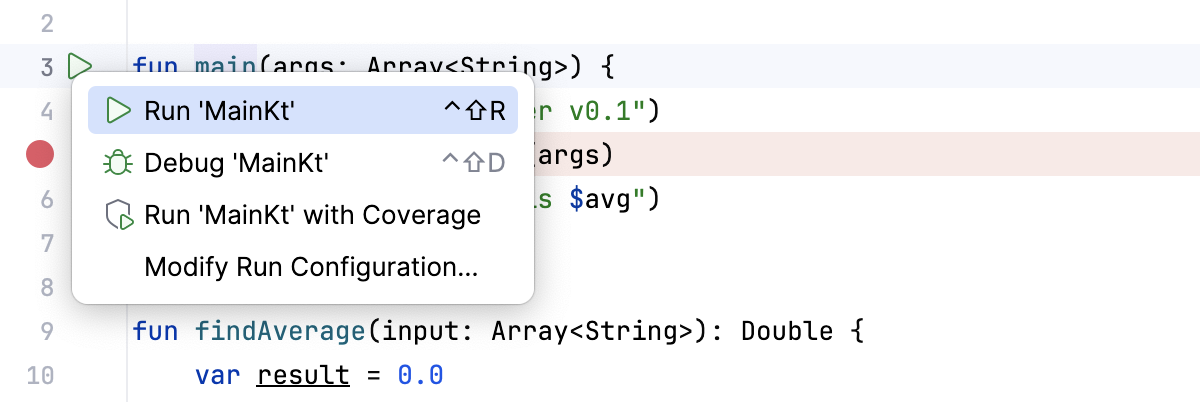
Verify that the program works correctly now.

Last modified: 23 October 2024