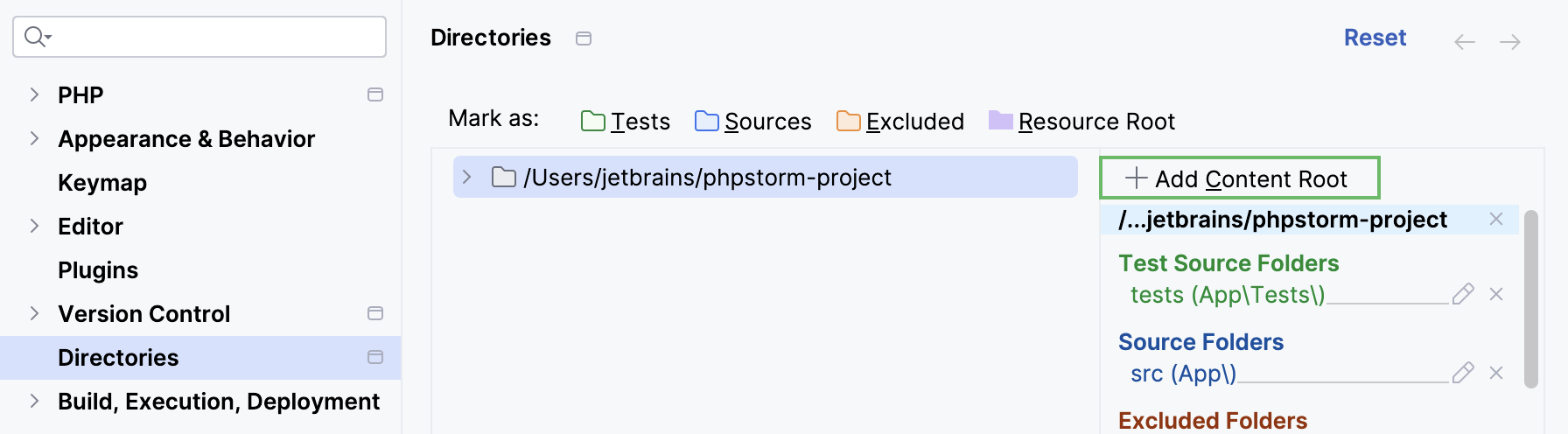
Directory structure
PhpStorm can distinguish between different folder types in a project directory structure. The folder type determines how PhpStorm treats the folder contents—for example, Sources folders are used as roots for namespace auto-completion, while Excluded folders are excluded from indexing.
The IDE marks folders in PHP projects with types automatically based on the contents of the composer.json file. You can also mark them manually in Settings (Ctrl+Alt+S) | Directories or from the Project tool window.
Folder types
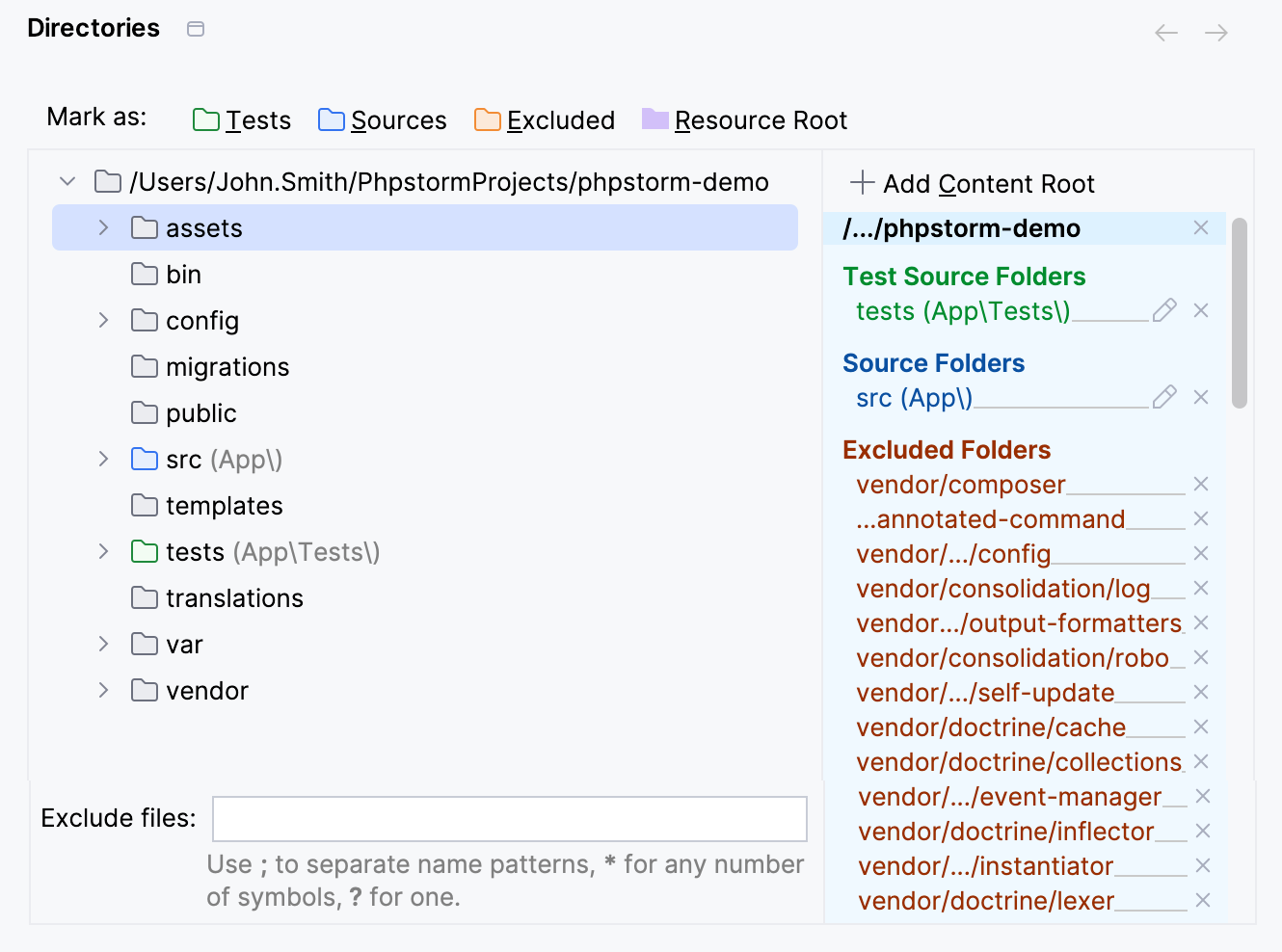
Tests
PhpStorm considers the contents of the Tests folder to be unit tests.
Sources
This is the root for PHP namespaces used in your project.
Based on this setting, PhpStorm suggests the proper folder name when you want to create a new namespace under another parent namespace during creation or moving of a PHP class, that is, when you are actually creating or moving a PHP class to a non-existing namespace under another parent namespace. If no Sources folder is specified, you will have to type the proper folder manually.
Excluded
Excluded folders are not involved in indexing, and therefore they are ignored during search, parsing, watching, and other operations.
Usually, one would like to exclude temporary build folders, generated output, logs, and other project output. Excluding the unnecessary paths is a good way to significantly improve performance.
Resource Root
Files and subfolders in a Resource Root folder can be referenced relative to this folder instead of specifying full paths to them.
Besides the explicitly set folder types, PhpStorm also detects and distinguishes the folders that contain library files, such as /vendor or /node_modules. Library folders are excluded from error checks, but still indexed, which means that the classes and methods from libraries are available in auto-completion, search, reference resolution, and so on, but on a second-class citizen principle.
To configure the list of PHP library folders (also referred to as Include paths in PhpStorm), go to Settings (Ctrl+Alt+S) | PHP and select the Include Path tab. For more information, see Configure include paths.
To learn more about configuring JavaScript libraries, refer to Configure JavaScript libraries.
Mark directories with a folder type
In the Settings dialog (Ctrl+Alt+S) , select Directories.
On the Directories page, click the desired content root in the right-hand pane. Directories under this content root are displayed as a tree view in the left-hand pane.
Select the directory and use its context menu or the Mark as toolbar to mark it as one of the available root types.
Mark directories in the Project tool window
Right-click the desired directory in the Project tool window.
From the context menu, point to Mark Directory As node.
Choose Mark as <directory status>.
Add a content root
The application root directory in PhpStorm is called a content root. You can add several content roots within one PhpStorm project.
Having several content roots enables you to work with files from several directories that do not have a common immediate parent. This is helpful when you use static contents, for example, icons. You can just save them all in a folder and then specify this folder as an extra content root in several projects.
In the Settings dialog (Ctrl+Alt+S) , click Directories.
On the Directories page, click
Add Content Root and set the path to the desired directory.