Build Solution
ReSharper allows you to build your solution incrementally using multiple parallel processes. You can use ReSharper Build as a replacement to Visual Studio's native's build management.
Note that ReSharper does not replace MSBuild — your projects are still built normally. The difference is that projects that do not need updating are not rebuilt.
Start ReSharper Build
By default, ReSharper Build is disabled. To enable it, do one of the following:
Go to the page of ReSharper options and choose ReSharper Build in the Build Engine section.
Open the Build & Run window() and then click Enable ReSharper Build.
When ReSharper Build is enabled, there are several ways to build your solution:
Use any of Visual Studio build commands — for example Ctrl+Shift+B — all these commands and shortcuts are overridden by ReSharper Build.
Click Build
 or choose other build command available in its drop-down menu on the toolbar of the ReSharper Build & Run window.
or choose other build command available in its drop-down menu on the toolbar of the ReSharper Build & Run window.To build, rebuild or clean a specific project, right-click it in the Build & Run window and choose the corresponding command in the context menu.
ReSharper also provides its own implementation of NuGet restorer, which works with all Visual Studio versions. By default, ReSharper makes sure that all related NuGet packages are restored before each build, but you can disable it by clearing the corresponding checkbox on the page of ReSharper options. If the automatic restore is disabled, you can always run it manually by clicking Restore NuGet packages ![]() on the toolbar of Build & Run window.
on the toolbar of Build & Run window.
NuGet restorer writes log to output if it is enabled on this options page. You can also configure log message level and view log information for restores on the page of ReSharper options.
Build process
When you run ReSharper Build for the first time, it builds all projects using multiple parallel processes according to your configuration. All build management happens out of process, so Visual Studio remains responsive while a build is running.
The next time you build the solution, ReSharper only builds projects where supported build items were changed. If the change affects public types used in other projects, the dependent projects are rebuilt as well.
The projects that are not affected by changes are skipped completely, including all additional build logic. If you want to execute pre-build and post-build events and/or BeforeBuild and AfterBuild MSBuild targets for skipped projects, use the corresponding checkboxes on the page of ReSharper options(Alt+R, O).
ReSharper Build maintains a dependency graph of inputs and outputs to MSBuild tasks, targets and projects, and efficiently monitors the file system for changes. When you start a build, ReSharper Build already knows if the timestamps are up to date, without having to invoke MSBuild: if a timestamp is up to date, the project is skipped.
By default, ReSharper Build uses the same MSBuild version as specified in Visual Studio settings and runs in 6 processes in parallel. If necessary, you can specify MSBuild version explicitly and change the number of processes on the page of ReSharper options(Alt+R, O).
Build process and summary are visualized in the Build & Run window:
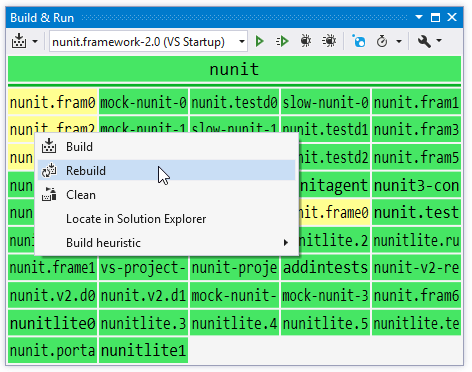
All projects of your solution are visualized in a grid, each of them having specific color. You can also hover the mouse over a project to display a tooltip explaining the state. Colors represent project build states:
Dark grey — the project is cleaned or never built.
Grey — the project is not built for one of the two reasons: it is excluded from the solution build, or you only run build for specific projects and unrelated projects are not built.
Light Blue — the project was built in the previous run and does not have any changes.
Blue — the project was built in the previous run and does not have any changes; projects that it references only have private changes.
Green — the project was changed or one of the dependent projects had public changes, then it was rebuilt successfully without warnings.
Yellow — the project was changed or one of the dependent projects had public changes, then it was rebuilt successfully with warnings.
Red — the project was changed or one of the dependent projects had public changes, then the project build failed.
If you need to cancel the current build, choose in the main menu.
Analyze build results
Once a build completes, ReSharper displays build errors (and optionally, warnings) in the Build Results window.
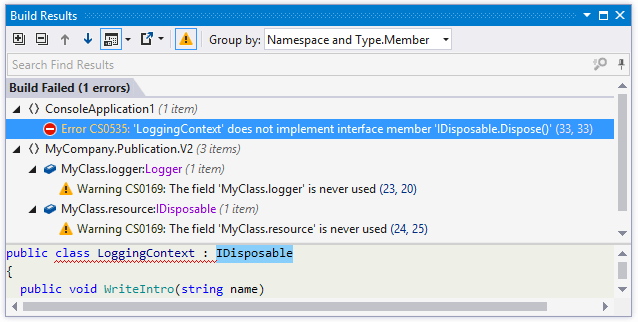
By default, results only appear if there are build errors. If necessary, you can use the Show build results... selector on the page of ReSharper options to display results with warnings, show results always or never.
In the Build Results window, you can further study build output in one of the following ways:
Choose a convenient way to group the results using one of multiple options in the Group by selector.
If there are build errors, only these errors appear in the window. If you also want to see compilation warnings, click Show Warnings
 on the toolbar.
on the toolbar.Use the Previous
 / Next
/ Next  buttons or Shift+F8/ F8 shortcuts to navigate between build messages.
buttons or Shift+F8/ F8 shortcuts to navigate between build messages.To preview code that originated an error or warning, click Show Preview
 or press Ctrl+P. In the preview pane, which can be located either on the left or on the bottom of the window, errors and warning are highlighted either with red or with a blue squiggle.
or press Ctrl+P. In the preview pane, which can be located either on the left or on the bottom of the window, errors and warning are highlighted either with red or with a blue squiggle.Double-click any error or warning to navigate to the corresponding code line in the editor.
Configure ReSharper Build
You can configure ReSharper Build on ReSharper options pages under .
You can disable ReSharper solution builder by clearing the ReSharper Build checkbox on the page of ReSharper options(Alt+R, O).
Exclude items from build
If you do not need to build some projects when you build your solution, you can exclude them to reduce build time. To do so, go to the page of ReSharper options and mark projects or solution folders that you want to exclude in the Projects that should never be built section. You can use the search box in this section to filter the solution tree to show only matching items.
Note that you would not be able to build excluded items, even if you invoke the Build command on these items in the Solution Explorer.
Excluding a project means it won’t get rebuilt, even if source files are out of date or a referenced project has public API changes. This is quite drastic, and can lead to uncaught compilation errors, but can be useful to temporarily exclude a project that is slow to compile, and not used in your current development task. It’s similar to unloading a project in Visual Studio so that it does not compile, but the source files are still available to ReSharper to allow for navigation and refactoring. We recommend re-enabling and rebuilding before committing to source control, or using Solution-Wide Analysis to show compile errors as you type.
Force specific projects to build
ReSharper Build does not build projects if they were built successfully before, and have not had any changes since them. If you need to build some projects independently of changes in them, you can force build them. To do so, mark projects or solution folders that you want to force build in the Projects that should always be built section. You can use the search box in this section to filter the solution tree to show only matching items.
Marking a project as 'always build' tells ReSharper Build to never apply heuristics to this project, but to always pass it to MSBuild. This does not mean that the project will always be rebuilt and recompiled, but it means MSBuild is always called - MSBuild will still check timestamps and might perform an incremental build. This is useful for projects that have custom build steps that ReSharper Build can’t track (although it would be better to rewrite the custom build steps as proper MSBuild targets that support incremental build.).
Visualisation settings
By default, when you start ReSharper build, the Build & Run window is brought up and build progress is also shown in the Visual Studio status bar. If necessary, you can configure this behavior on the page of ReSharper options.
Supported build items
When evaluating changes in a previously built project to decide whether to rebuild it, ReSharper checks build items of the most common MSBuild items types:
Changes in build items of the type None and other types not listed above are ignored by default. If your project build relies on other custom build item types, names of these types should be registered with AvailableItemName in the .csproj/ .vbproj file, e.g:
Supported project types and limitations of ReSharper Build
ReSharper Build supports most .NET project types and languages that are MSBuild-based (C#, VB.NET, F#, C++), including .NET Core projects. However, there are following limitations:
Non-MSBuild projects. ReSharper Build cannot work with project types that are not MSBuild-based. This includes Web Sites (folder based projects, not MVC web applications), WinJS applications and DNX applications. If there are projects of these types in your solution, the whole solution build will fall back to the standard MSBuild build process.
Custom build steps. Typically, custom build steps (including pre- and post-build steps in C++ projects) are the equivalent of calling a batch file, with several command lines being executed to, for example, copy files to the output directory. These are a black box as far as ReSharper Build is concerned — it does not know what is happening in the custom build step, so can’t track the input and output. Furthermore, if the project is skipped, the build step does not run, which could cause issues with the build (this is the main reason ReSharper Build is disabled by default).
However, custom MSBuild targets and tasks WILL work with ReSharper Build, as long as the custom target and task supports incremental building, with a list of inputs and outputs that can be monitored for timestamp changes. Converting a naive custom build step to custom targets is highly recommended in order to get good results with ReSharper Build.
If a custom build step cannot be replaced, the project can be added to the list of projects that should be 'always built', without having heuristics applied, meaning they are always passed to MSBuild, and MSBuild’s standard incremental build process will run. This can be configured on the page of ReSharper options.