Run/debug configurations
GoLand uses run/debug configurations to run, debug, and test your code. Each configuration is a named set of startup properties that define what to execute and what parameters and environment should be used.
There are two types of run/debug configurations:
Temporary — created every time you run or debug functions or tests.
Permanent — created explicitly from a template or by saving a temporary configuration. Permanent configurations remain as part of your project until you remove them.
Whenever you run, debug, or test your code, GoLand either uses an existing permanent run/debug configuration or creates a new temporary one.
Permanent configurations have opaque icons while the icons of temporary configurations are semi-transparent. The red cross over the configuration icon indicates an error in configuration settings.
The maximum number of temporary configurations is 5. The older ones are automatically deleted when new ones are added. If necessary, you can increase this limit in .
Create temporary run/debug configurations
To create a temporary run/debug configuration, you can run your code from the gutter or from the context menu.
Run from the editor
If you are not going to pass any parameters to your program, and your program does not require any specific actions to be performed before start, you can run it right from the editor.
Click
in the gutter near the
mainfunction and select Run.To run a script, open it in the editor or select it in the Project tool window, and then select Run <script file name> from the context menu.
Create permanent run/debug configurations
GoLand provides the following ways to create a permanent run/debug configuration:
Create from a template or copy an existing configuration.
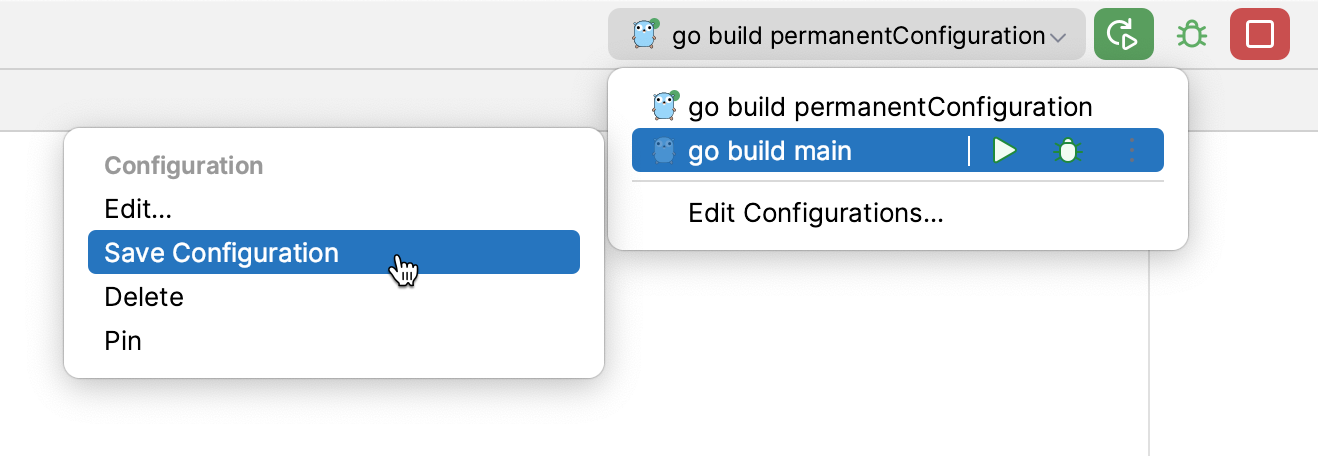
Save a temporary configuration as permanent
Select a temporary configuration in the run/debug configuration switcher, click
/
and select Save Configuration.
Alternatively, select a temporary configuration in the Run/debug configurations dialog and click
on the toolbar.
GoLand provides run/debug configuration templates for different languages, tools, and frameworks. The list of available templates varies depending on the installed and enabled plugins.
Create a run/debug configuration from a template
Go to . Alternatively, press Alt+Shift+F10, then 0.
In the Run/Debug Configurations dialog, click
on the toolbar or press Alt+Insert. The list shows the run/debug configuration templates. Select Go build.
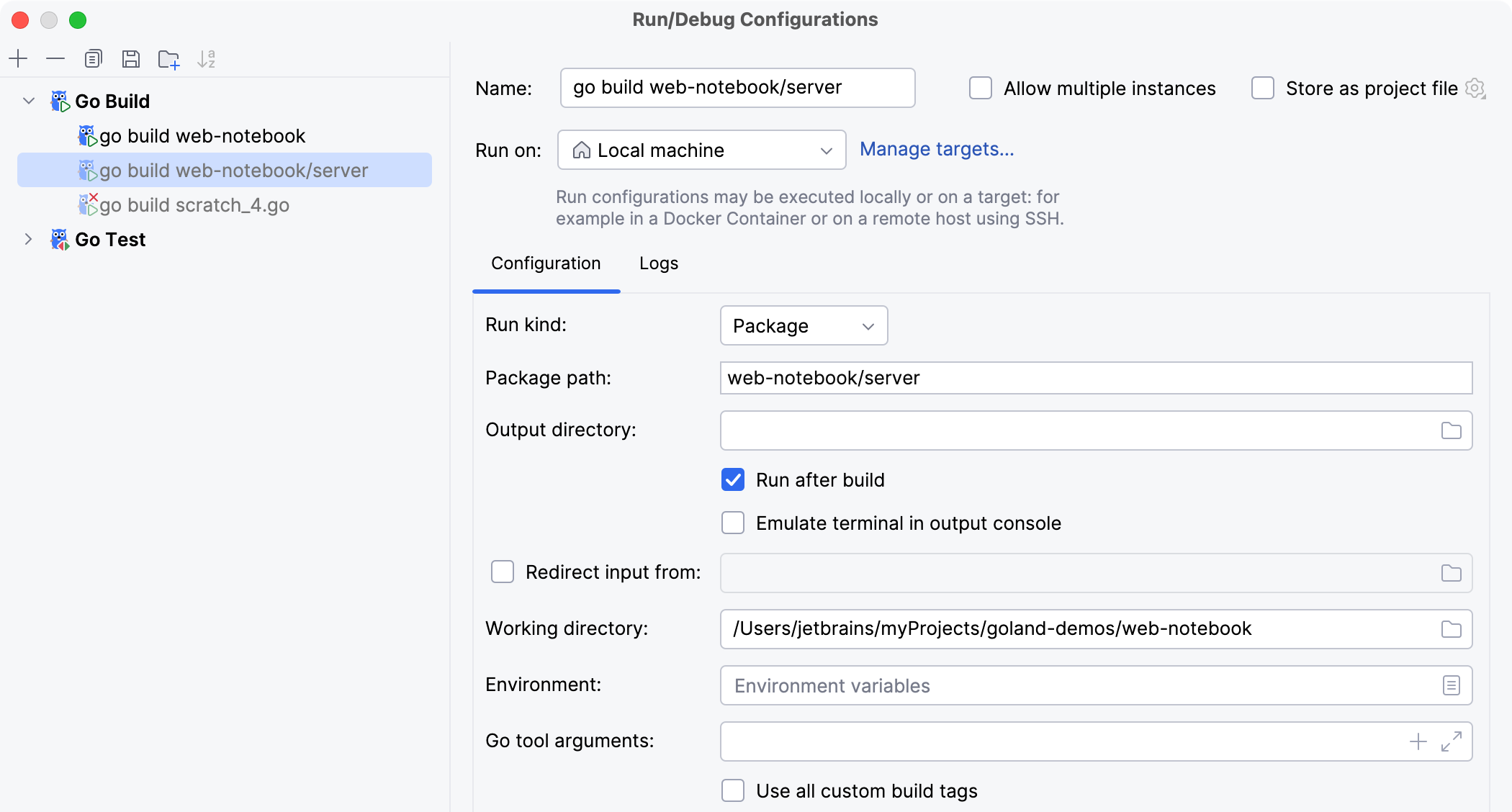
Specify the run/debug configuration name in the Name field. This name will be used to identify the run/debug configuration in lists and menus.
On the Configuration tab, you can set the following options:
In the Before launch section, define whether you want to perform any specific actions before launching the application, for example, launch an external tool or another build configuration before run. To skip the build stage, remove Build from the Before launch list .
You can either run the configuration right away or save the configuration to run it later.
To save the run configuration for later, click OK.
To run the configuration right away, click Run.
List of fields in Go Build configuration
Name | Description |
|---|---|
Run kind | Building scope for your application. File and Package scopes work similarly in tests and compilation/running configurations (in terms of the scope they cover).
|
Package path | Full import path of the package that you want to compile (for example, You can press Ctrl+Space to see a list of available packages. 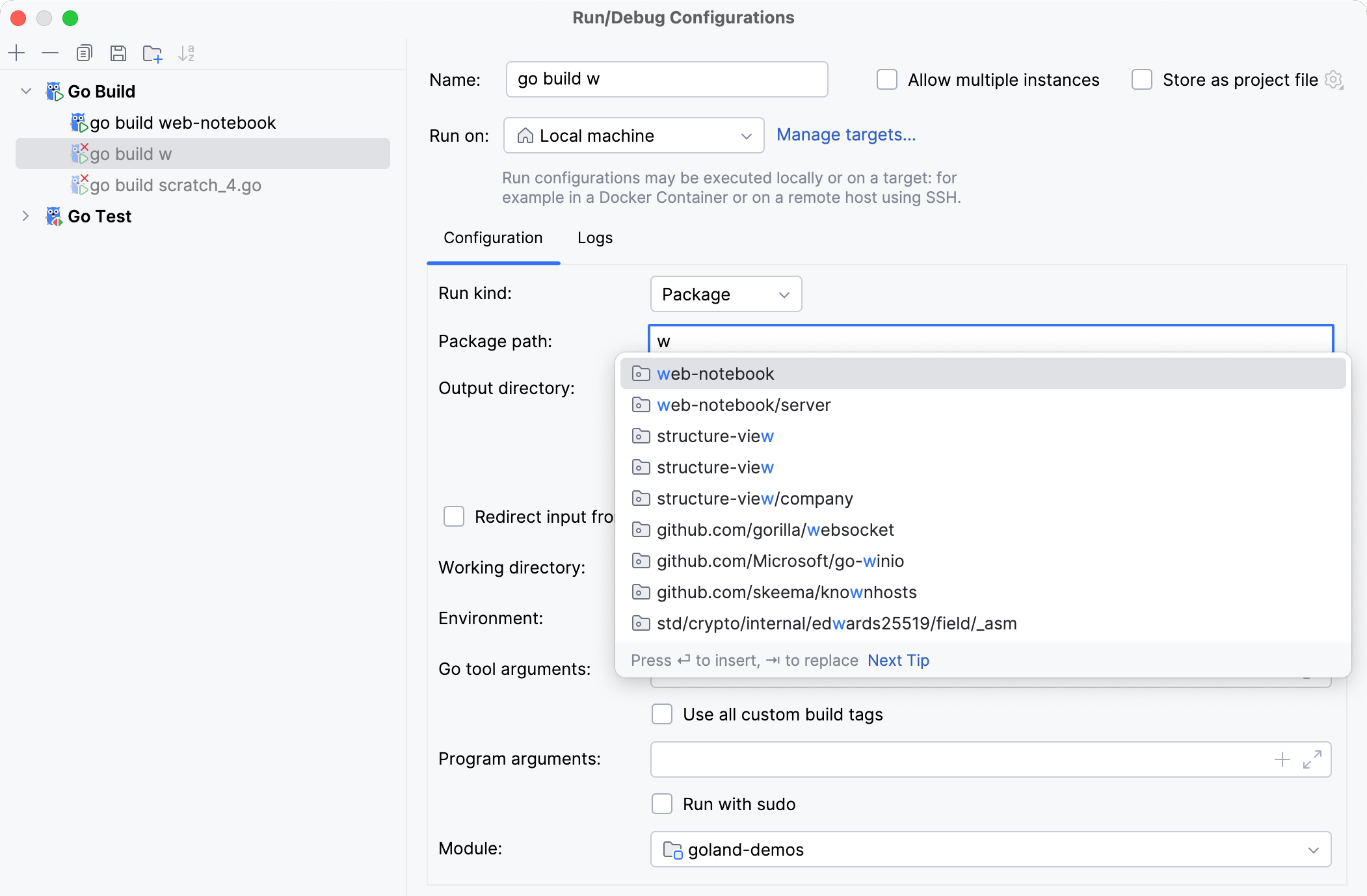 |
Output directory | Path to a directory where you want to output the executable file. |
Run after build | Execute the application after the build. |
Emulate terminal in output console | Executes the application and displays the output in the Run tool window as it would appear in the terminal.  |
Redirect input from | File to read the input from. |
Working directory | Directory that is used for the built application. If you have any code that creates relative files or directories, they will be relative to this directory. |
Environment | Environment variables for your application. To edit environment variables, click the Browse button at the end of the field. In the Environment Variables dialog, click the Add button and add the environment variables that you need. 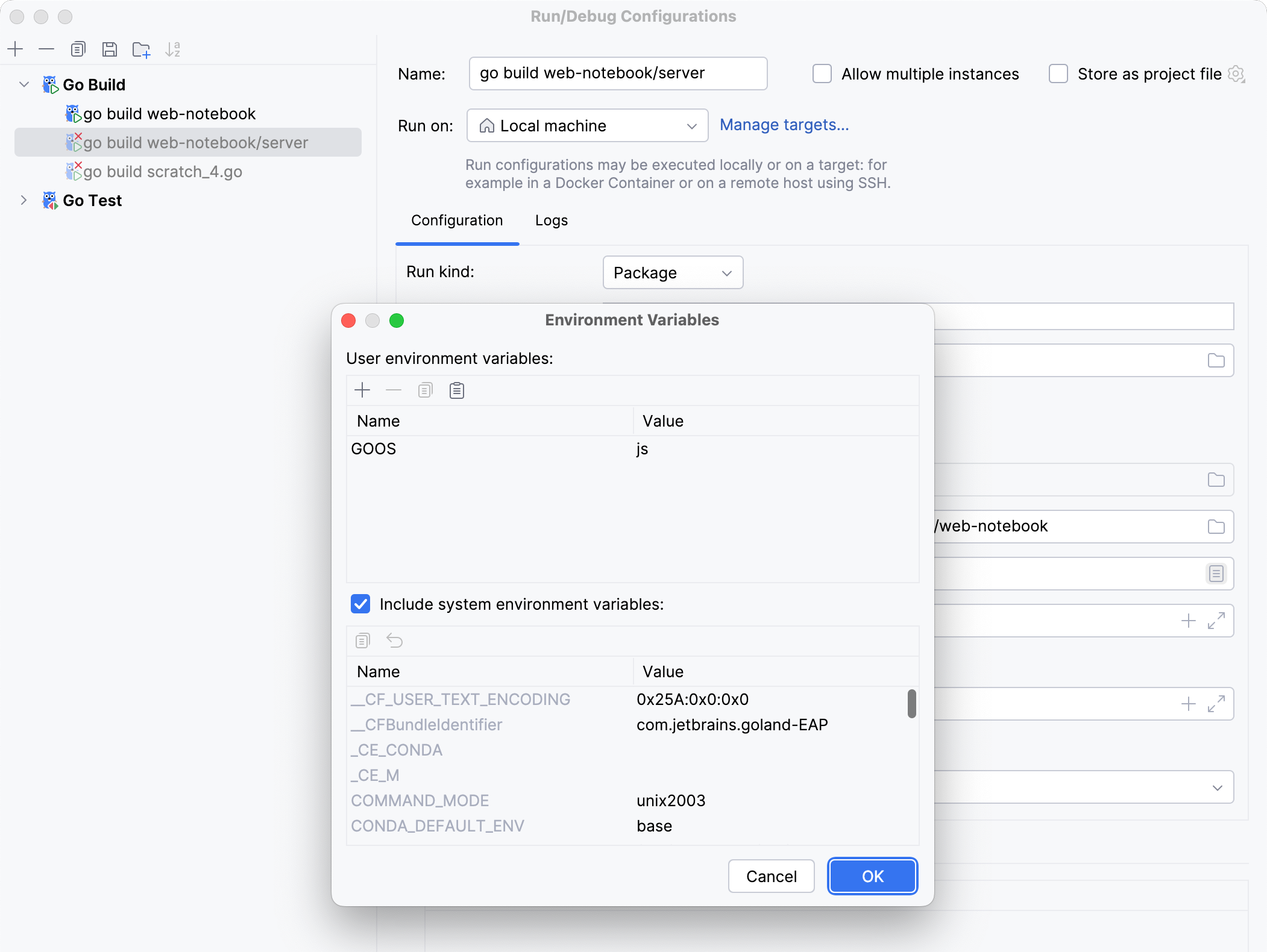 |
Go tool arguments | Arguments for the go tool (for example, |
Use all custom build tags | All tags that are applied during the build. Tags are listed in settings Ctrl+Alt+S under . |
Program arguments | Arguments for the built application. Also, you can use macros in this field. |
Run with sudo | Run the application with elevated privileges. |
Module | Name of the current module. |
Before launch | Add tasks that you want to launch before the launch of the selected run/debug configuration. To add a task click the Add button Alt+Insert and select the tool that you want to add. |
Store as project file | Enable this option to save your configuration as a project file and share it with team members through VCS. |
List of fields in Go Test configurations
Name | Description |
|---|---|
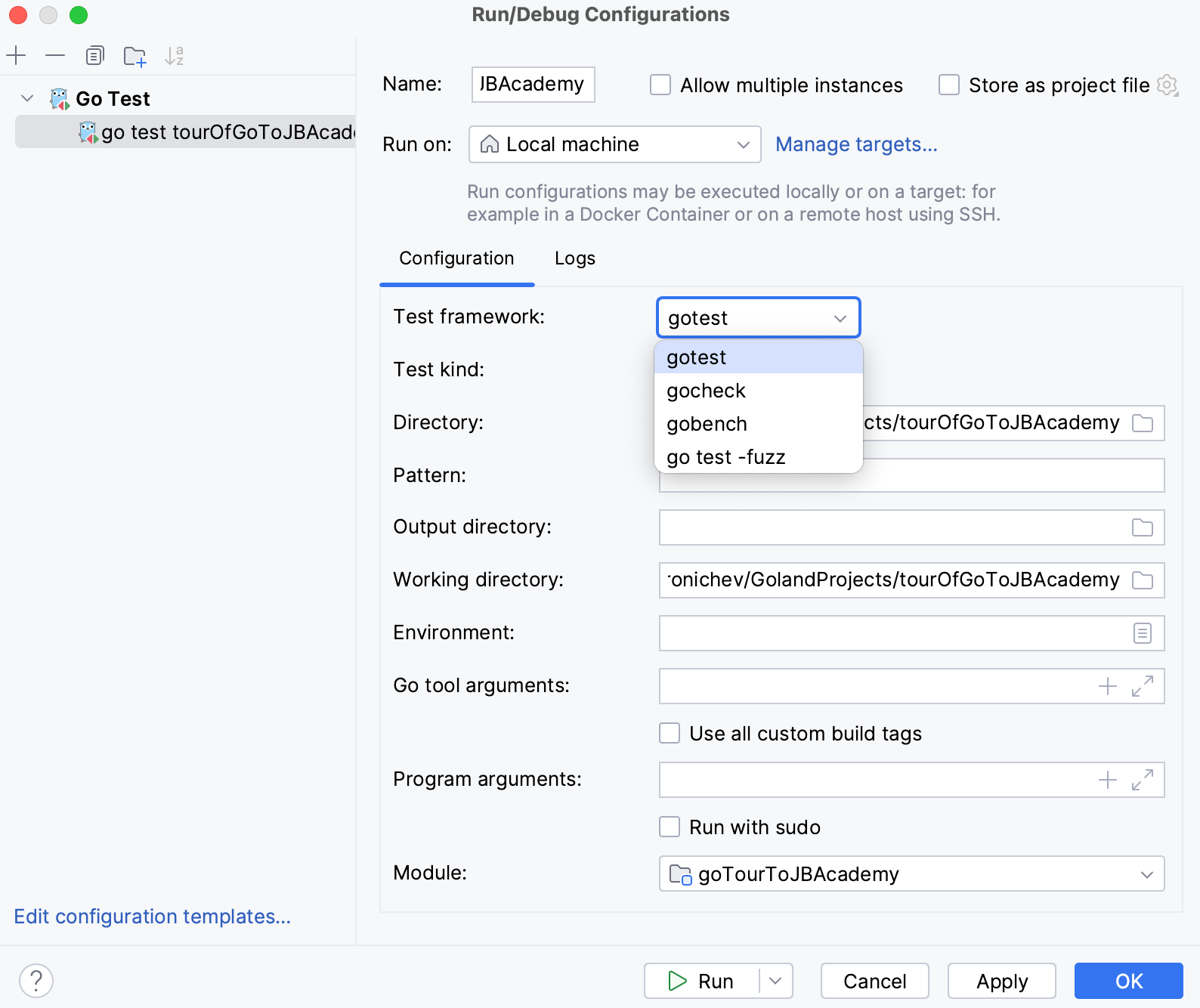
Test framework | Select the package that you want to use to run tests.
 |
Test kind | Select the scope from which you want to run tests:
|
Pattern | Type a regular expression that defines what tests to run. GoLand will execute only the tests, examples, and fuzz tests that conform to the regular expression provided. For tests, the expression is divided by slashes ( For instance, to execute a specific test named 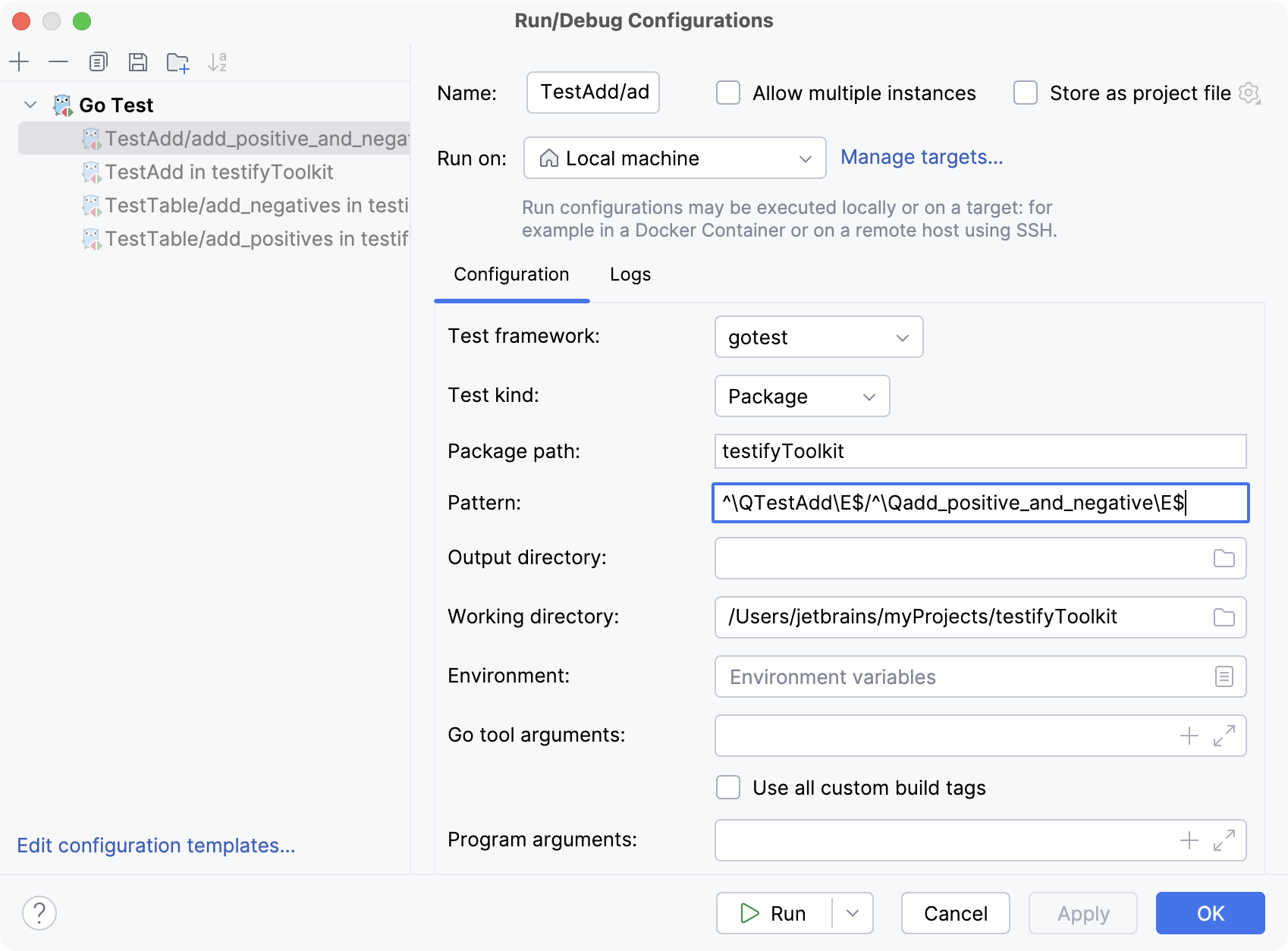 |
Working directory | Directory that is used for the built application. If you have any code that creates relative files or directories, they will be relative to this directory. |
Output directory | Directory that stores your test results if any. |
Run after build | Execute a test after the build. |
Redirect input from | Path to the file that will to take program input instead of the console. |
Working directory | Directory that is used for the built application. If you have any code that creates relative files or directories, they will be relative to this directory. |
Environment | : environment variables that you need to run the test. To edit environment variables, click the Browse button at the end of the field. In the Environment Variables dialog, click the Add button and add the environment variables that you need.  |
Go tool arguments | Arguments for the go tool (for example, |
Use all custom build tags | All tags that are applied during the build. Tags are listed in settings Ctrl+Alt+S under . |
Program arguments | Arguments for the test. |
Run with sudo | Grant sudo privileges to the test. |
Before launch: Activate tool window | Add tasks that you want to launch before the launch of the selected run/debug configuration. To add a task, click the Add button Alt+Insert and select the tool that you want to add. |
Before launch
In this area, you can specify tasks to be performed before starting the selected run/debug configuration. The tasks are performed in the order they appear in the list.
Item | Shortcut | Description |
|---|---|---|
Alt+Insert | Click this icon to add one of the following available tasks:
| |
Alt+Delete | Click this icon to remove the selected task from the list. | |
Enter | Click this icon to edit the selected task. Make the necessary changes in the dialog that opens. | |
Alt+Up Alt+Down | Click these icons to move the selected task one line up or down in the list. The tasks are performed in the order that they appear in the list. | |
Show this page | Select this checkbox to show the run/debug configuration settings prior to actually starting the run/debug configuration. | |
Activate tool window | By default this checkbox is selected and the Run or the Debug tool window opens when you start the run/debug configuration. Otherwise, if the checkbox is cleared, the tool window is hidden. However, when the configuration is running, you can open the corresponding tool window for it yourself by pressing Alt+4 or Alt+5. |
Launch a run configuration
You can launch existing run configurations in one of the following ways:
If the run configuration is already selected in the Run widget, click
next to it or press Shift+F10.
If you want to select another run configuration, click the Run widget. In the menu that opens, click
next to the run configuration you want to launch.
Press Alt+Shift+F10. In the menu that opens, click the run configuration you want to launch.
Share run/debug configurations
You might want to share your run/debug configurations so that your teammates could run the application using the same configuration or enable them to remotely attach to the process you are running.
GoLand provides a mechanism to store your run/debug configurations as project files and share them through VCS. The same mechanism can also be used when you want to send your configuration as a file to someone else, create a local backup of your run/debug configurations, or import them from a file.
Go to . Alternatively, press Alt+Shift+F10, then 0.
Select the run/debug configuration you want to share, enable the Store as project file option, and specify the location where the configuration file will be stored.
You can configure any location unless compatibility with GoLand 2019.3 and earlier is required. For compatibility with these versions, store the file in the suggested location.
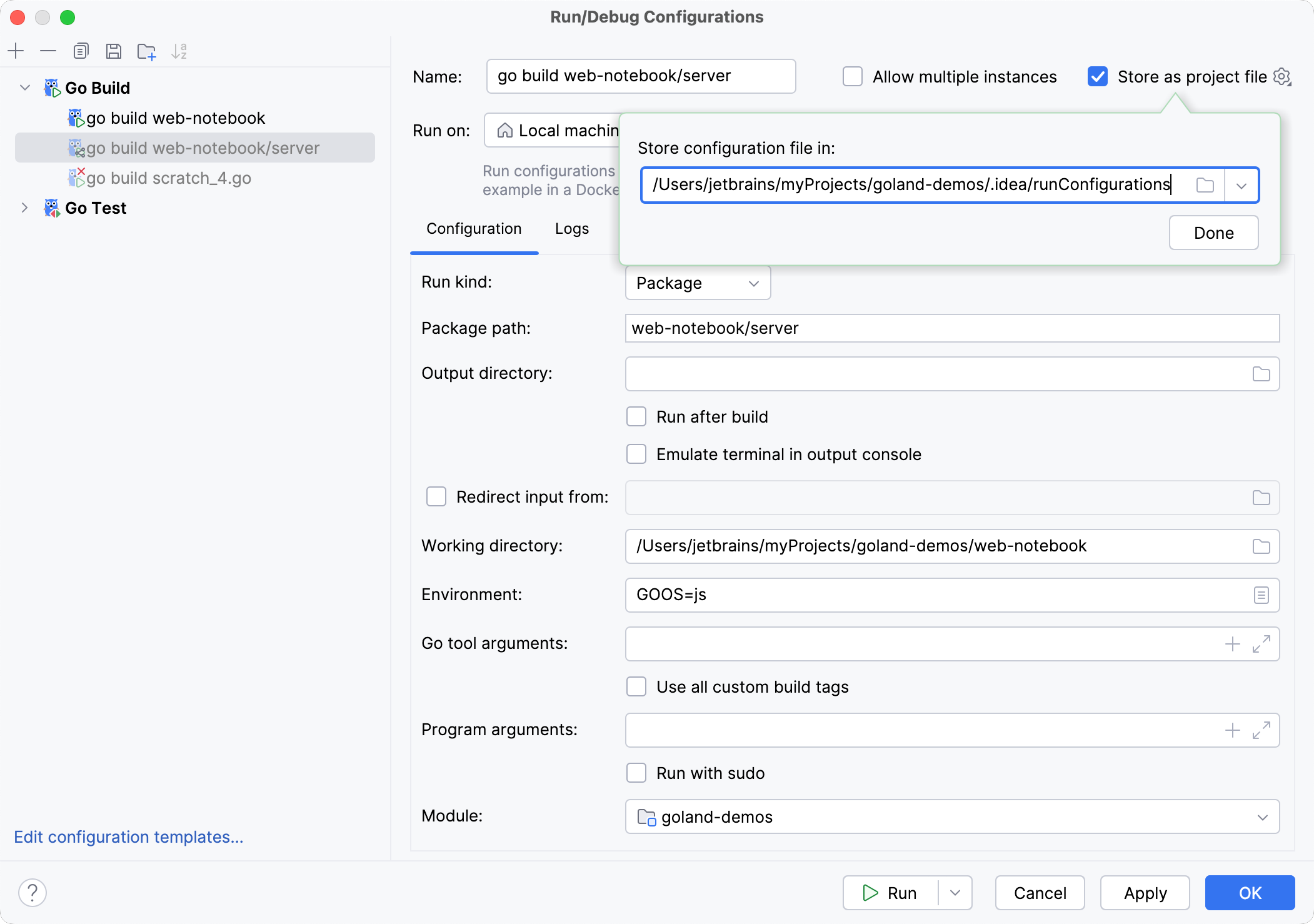
(Optional) If the .idea directory is added to VCS ignored files, the .idea/runConfigurations subfolder will be ignored, too. If the project uses Git, you can share .idea/runConfigurations and leave .idea ignored by modifying .gitignore as follows:
/.idea/* !/.idea/runConfigurations
Run/debug configuration templates
All run/debug configurations are based on templates, which implement the startup logic, define the list of parameters and their default values. The list of available templates is predefined in the installation and can only be extended via plugins. However, you can edit default parameter values in each template to facilitate the setup of new run/debug configurations.
Configure the default values for a template
Go to . Alternatively, press Alt+Shift+F10, then 0.
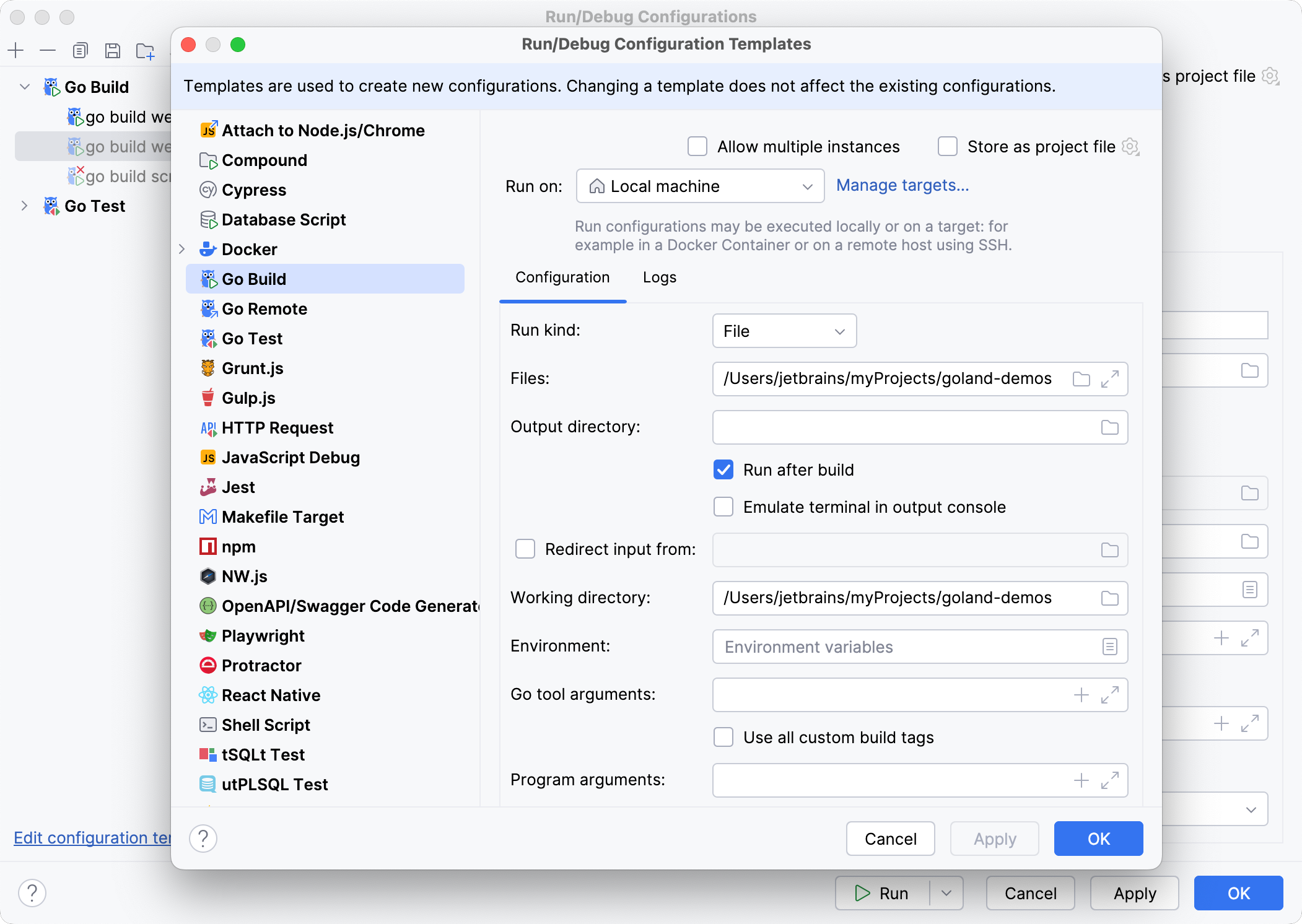
In the left-hand pane of the run/debug configuration dialog, click Edit configuration templates.
In the Run/Debug Configuration Templates dialog that opens, select a configuration type.
Specify the desired default parameters and click OK to save the template.
Run/debug configuration folders
When there are many run/debug configurations of the same type, you can group them in folders for easier access.
Create a folder for run/debug configurations
Go to . Alternatively, press Alt+Shift+F10, then 0.
In the Run/Debug Configurations dialog, select a configuration type and click
on the toolbar. A new empty folder for the selected type is created.
Specify the folder name in the text field to the right or accept the default name.
Select the desired run/debug configurations and move them under the target folder.
Apply the changes. If a folder is empty, it will not be saved.
When you no longer need a folder, you can delete it Delete. The run/debug configurations grouped under this folder will be moved under the root of the corresponding run/debug configuration type.